問題
出典:「令和4年度第一種電気主任技術者一次試験 理論科目 A問題 問2」
次の文章は,電磁誘導に関する記述である。文中の に当てはまる最も適切なものを解答群の中から選べ。ただし, E, Bはそれぞれ電界ベクトル及び磁束密度ベクトルを表す。
一般に,空間に固定されたループ(閉曲線) Cに発生する起電力 Vは,
V=\(\oint_S\mathbf E\cdot d\mathbf l=0\)⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ①
と表される。ここで, dlはループに沿った線素ベクトルである。 (1) の定理を適用すると,①式は,
V=\(\int_S\mathbf (∇×E)⋅n\cdot d\mathbf S=0\) ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ①′
と変形できる。ただし, Sはループ Cに囲まれた面, nはその面の単位法線ベクトル, dSは面素である。磁束密度 Bが時間 tに応じて変化する場合には,マクスウェル方程式
∇×E= (2) ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ②
を ①′式に代入し,面 Sを貫く磁束は Φ=∫SB⋅ndSと表せることを用いると,
V= (3) ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ①′′
のようにファラデーの法則が得られる。
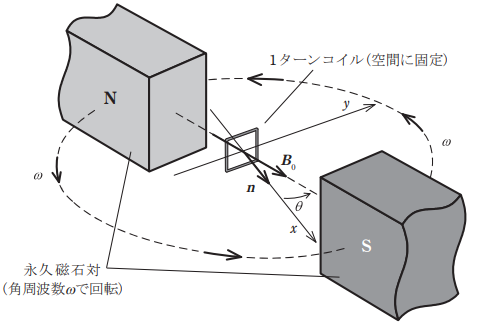
図のように,座標原点を中心として対向する永久磁石が形成する一様な磁束密度 \(B_0\) の中に,一辺の長さが aの正方形状の 1ターンコイルが設置されており,コイル面の法線ベクトルは x軸の方向を向いている。永久磁石対は座標原点を中心として xy平面内を角速度 ωで回転しており,磁界と x軸とのなす角は θ=ωtと表される。このとき,磁束密度のコイル面法線方向成分は B⋅n= (4) となるので,上記の関係式を用いてコイルに発生する交流起電力を求めることができる。
例えば, 1 Tの磁束密度を発生する永久磁石対が毎分 3 000回転している場合を考えると,一辺の長さ a=10 cmの正方形状の 1ターンコイルに発生する交流起電力の振幅はおよそ (5) Vとなる。
〔問2の解答群〕
| (イ)\(B_0sinωt\) | (ロ)E×B | (ハ)\(B_0cosωt\) |
| (ニ)\(B_0tanωt\) | (ホ)300 | (ヘ)ガウス |
| (ト)3 | (チ)\(−\intΦdt\) | (リ)\(-\frac{dΦ}{dt}\) |
| (ヌ)∇⋅B | (ル)ストークス | (ヲ)ヘルムホルツ |
| (ワ)∇×B | (カ)0.03 | (ヨ)\(-\frac{\partial B}{\partial t}\) |
解答
(1) (ル)$$ストークス$$
(2) (ョ)$$-\frac{\partial B}{\partial t}$$
(3) (リ)$$-\frac{dΦ}{dt}$$
(4) (ハ)$$B_0cosωt$$
(5) (ト)$$3$$